翻译：pytorch官网60分钟教程（1.2.0）

译者博客：https://zinw623.github.io/

什么是PYTORCH?

它是基于python的科学计算包，读者定位为两种：

替代使用Numpy来使用GPU的功能
最灵活快速的深度学习研究平台

准备开始

Tensors

Tensors是类似于加上能在GPU上进行加速计算功能的Numpy的ndarrays。

1 2	from __future__ import print_function import torch

注意：
未初始化的矩阵被声明，但是在使用前不会包含确切的已知的值。当一个未初始化的矩阵被创建，分配内存中当时的任何值都将作为初始值出现。

构建一个5x3的矩阵，未初始化：

1 2	x = torch.empty(5, 3) print(x)

输出:

tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])

构建一个随机的初始化过的矩阵：

1 2	x = torch.rand(5, 3) print(x)

输出：

tensor([[0.6259, 0.0797, 0.8297],
        [0.6732, 0.7944, 0.2363],
        [0.6775, 0.2497, 0.3846],
        [0.8515, 0.5171, 0.6957],
        [0.7759, 0.6000, 0.1323]])

构建一个dtype为long且用0填充的矩阵：

1 2	x = torch.zeros(5, 3, dtype=torch.long) print(x)

输出：

tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])

构建一个直接从data里构建tensor：

1 2	x = torch.tensor([5.5, 3]) print(x)

输出：

tensor([5.5000, 3.0000])

或者从已有的tensor创建tensor。这些方法将重用输入tensor的内容，例如dtype，除非使用者提供新的值。

x = x.new_ones(5, 3, dtype = torch.double) # new_*方法接受了大小（sizes）
print(x)

x = torch.randn_like(x, dtype = torch.float) # 重写了dtype
print(x)                                     # 结构具有相同的size

输出：

tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)
tensor([[ 0.5955, -0.2528, -0.2648],
        [ 0.7689,  0.2396, -0.0121],
        [ 1.3478,  0.0460,  0.0255],
        [ 0.1266, -1.1526, -0.5546],
        [-0.2001, -0.0542, -0.6439]])

得到它的size（大小）：

1	print(x.size())

输出：

torch.Size([5, 3])

注意：
torch.Size事实上是元组，所以它支持所有的元组操作。

操作

有多种操作的语法。在下面的例子里，我们将看一下加法操作。

加法：语法1

1 2	y = torch.rand(5, 3) print(x + y)

输出：

tensor([[ 1.1550,  0.5950, -0.0519],
        [ 1.3954,  0.9232,  0.8904],
        [ 1.7020,  0.8187,  0.0265],
        [ 0.3831, -0.6057, -0.2829],
        [ 0.5647,  0.5976,  0.1128]])

加法：语法2

1	print(torch.add(x, y))

输出：

tensor([[ 1.1550,  0.5950, -0.0519],
        [ 1.3954,  0.9232,  0.8904],
        [ 1.7020,  0.8187,  0.0265],
        [ 0.3831, -0.6057, -0.2829],
        [ 0.5647,  0.5976,  0.1128]])

加法：提供一个输出向量作为参数

1
2
3

result = torch.emtpy(5, 3)
torch.add(x, y, out = result)
print(result)

输出：

tensor([[ 1.1550,  0.5950, -0.0519],
        [ 1.3954,  0.9232,  0.8904],
        [ 1.7020,  0.8187,  0.0265],
        [ 0.3831, -0.6057, -0.2829],
        [ 0.5647,  0.5976,  0.1128]])

加法：in-place

1 2	# 把x加到y上 y.add_(x)

输出：

tensor([[ 1.1550,  0.5950, -0.0519],
        [ 1.3954,  0.9232,  0.8904],
        [ 1.7020,  0.8187,  0.0265],
        [ 0.3831, -0.6057, -0.2829],
        [ 0.5647,  0.5976,  0.1128]])

注意：
任何改变张量的in-place操作后固定带一个_。例如：x.copy_(y),x.t_()，将改变x的值。

你可以使用类似于标准的numpy索引的所有附加功能。

1	print(x[:, 1])

输出：

tensor([-0.2528,  0.2396,  0.0460, -1.1526, -0.0542])

改变大小：如果你想resize/reshape张量，你可以使用torch.view:

x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8)  # size -1 从其他维度推断
print(x.size(), y.size(), z.size())

输出：

torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])

如果你有一个元素的张量，可以使用.item()获得python number的值。

1
2
3

x = torch.randn(1)
print(x)
print(x.item())

输出：

tensor([-0.8748])
-0.8748161792755127

然后阅读：
100+张量操作，here

numpy桥

将Torch Tensor转换成numpy array，反之也很简单。

Torch Tensor和numpy array潜在地共享内存（如果torch tensor在CPU上），并且改变一个将会使另一个改变。

将NumPy Array转换成Torch Tensor

看如何通过改变np array自动地改变Torch Tensor。

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out = a)
print(a)
print(b)

输出：

[2. 2. 2. 2. 2.]
tensor([2., 2., 2., 2., 2.], dtype=torch.float64)

CUDA张量

tensors可以通过.to方法被移动到任何设备。

# 只有CUDA可用时运行这个cell
# 我们使用"torch.device"控制张量出入GPU
if torch.cuda.is_available():
    device = torch.device("cuda")           # 一个CUDA device对象
    y = torch.ones_like(x, device = device) # 直接在GPU上创建tensor
    x = x.to(device)                        # 或者使用字符串".to("cuda")"
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))        # ''.to''也能一起改变dtype

输出：

tensor([0.1252], device='cuda:0')
tensor([0.1252], dtype=torch.float64)

AUTOGRAD:自动求导

[原英文网站]

Pytorch所有神经网络的核心是autograd包。让我们简单地看一下这个，然后我们将要去训练我们的第一个神经网络。

autograd包为所有tensors操作提供自动求导。它是一个定义即运行的框架，这以为着你的代码如何运行你的反向传播就如何被定义，每一次迭代都可以不同。

让我们用更简单的术语和一些例子来看看。

Tensor

torch.Tensor是包的核心类。如果你设置了它的属性.requires_grad为True，它开始时会追踪所有作用在它之上的操作。当你完成你的计算时你可以通过调用.backward()并且自动地计算所有梯度。这个张量的梯度将会被累积到.grad这个属性里。

为了组织张量追踪历史，你可以调用.detach()来从计算历史中将它分离，并且防止了在未来计算中被追踪。

为了防止追踪历史（并且使用内存），你也可以将代码块包装到with torch.no_grad():。这在当评估模型时非常有帮助，因为模型可能有requires_grad=True的可训练参数，但是我们并不需要梯度。

为了autograd的执行还有另一个非常重要的类 - Function。

Tensor和Function是相互关联的并且建立一个无环图，这图编码了计算的完整历史。每一个张量都有一个.grad_fn属性，参照了创建这个Tensor的Function（除了被用户创建的张量 - 它们的grad_fn is None）。

如果你想要计算衍生物，你可以调用一个Tensor的.backward()方法。如果Tensor是一个标量（即只有一个元素），你不需要为.backward()指定任何参数，然而如果它有更多的元素，你需要指定一个gradient参数，它是一个匹配形状的张量。

1	import torch

创建一个张量并且设置requires_grad=True并追踪它的计算。

1 2	x = torch.ones(2, 2, requires_grad=True) print(x)

输出：

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

进行一个张量计算：

1 2	y = x + 2 print(y)

输出：

tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)

y作为一个操作的结果被创建，所以它有一个grad_fn。

1	print(y.grad_fn)

输出：

<AddBackward0 object at 0x7f3772e36588>

对y做更多的操作

z = y * y * 3
out = z.mean()

print(z, out)

输出：

tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)

.requires_grad_( ... )in-place改变已存在张量的requires_grad=True标示。如果没有给定输入默认的标示是False。

a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

输出：

False
True
<SumBackward0 object at 0x7f3772e36dd8>

梯度

现在开始反向传播。因为out包含一个单独的标量，out.backward()等价于out.backward(torch.tensor(1.))。

1	out.backward()

打印梯度d(out)/dx

1	print(x.grad)

输出：

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

你应当有一个4.5的矩阵。让我们调用out的张量“o”，我们有$o=\frac{1}{4}\sum_{i}z_i,z_i=3(x_i+2)^2$和$z_i\mid_{x_i=1}=27$。然而，$\frac{\partial{o}}{\partial{x_i}}\mid_{x_i=1}=\frac{9}{2}=4.5$。

数学上的，如果你有一个向量值的函数$\vec{y}=f(\vec{x})$，然后$\vec{y}$关于$\vec{x}$的梯度是雅克比矩阵：

$$
J =
\left[
\begin{matrix}
\frac{\partial{y_1}}{\partial{x_1}} & \cdots &\frac{\partial{y_1}}{\partial{x_n}} \
\vdots & \ddots & \vdots \
\frac{\partial{y_m}}{\partial{x_1}} & \cdots & \frac{\partial{y_m}}{\partial{x_n}} \
\end{matrix}
\right]
$$

总的来说，torch.autograd是为了计算向量-雅克比积(vector-Jacobian product)。那是给定向量$v=(v_1 v_2 \cdots v_m)^T$，计算积$v^T \cdot J$。如果$v$恰好是标量函数$l=g(\vec{y})$的梯度，就是$v=(\frac{\partial{l}}{\partial{y_1}}\cdots\frac{\partial{l}}{\partial{y_m}})^T$，然后通过链式法则，向量-雅克比积将会成为$l$关于$\vec{x}$的梯度：

$$
J^T\cdot v =
\left[
\begin{matrix}
\frac{\partial{y_1}}{\partial{x_1}} & \cdots &\frac{\partial{y_1}}{\partial{x_n}} \
\vdots & \ddots & \vdots \
\frac{\partial{y_m}}{\partial{x_1}} & \cdots & \frac{\partial{y_m}}{\partial{x_n}} \
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{\partial{l}}{\partial{y_1}} \
\vdots \
\frac{\partial{l}}{\partial{y_m}}
\end{matrix}
\right]=
\left[
\begin{matrix}
\frac{\partial{l}}{\partial{x_1}} \
\vdots \
\frac{\partial{l}}{\partial{x_n}}
\end{matrix}
\right]
$$

（注意：$v^T\cdot J$给出了一个行向量，这个可以通过$J^T\cdot v$得到列向量。）

向量-雅克比积的这个特征使得给一个非标量输出的模型输入一个的外部梯度非常便捷。

现在让我们看看一个向量-雅克比积的例子。

x = torch.randn(3, requires_grad = True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

输出：

tensor([-1350.9803,   805.9799,  -188.3773], grad_fn=<MulBackward0>)

现在y不在是标量，torch.autograd不能直接计算完整的雅克比矩阵，但是如果我们只是想要向量-雅克比积，只需简单地输入一个向量给backward作为参数。

v = torch.tensor([0.1, 1.0, 0.0001], dtype = torch.float)
y.backward(v)

print(x.grad)

输出：

tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

你也能通过把代码块封装到with torch.no_grad():中来停止autograd追踪带有.requires_grad=True的张量。

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

输出:

True
True
False

神经网络

[原英文网站]

神经网络可以通过torch.nn包来构建。

现在你看一眼autograd，nn依赖于autograd来定义模型并且对他们求导。一个nn.Module包括层（layers)和一个forward(input)方法，这个方法会返回outupt。

例如，看这个分类数字图像的网络：

卷积网络

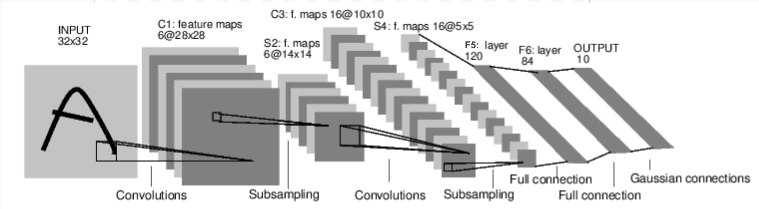
这是一个简单的前馈神经网络。它接受一个输入，将它输入穿过许多层然后一个接着另一个，然后最后给出一个输出。

一个典型的神经网络的训练流程如下：

定义一个带有许多可学习的参数（或权重）的神经网络。
在输入的训练集上迭代。
通过网络处理输入。
计算损失（loss 输出与正确有多远）。
反向传播求网络的梯度。
更新网络权重，典使用一个简单典型的更新规则：weight = weight - learning_rate * gradient

定义网络

让我们来定义网络：

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1是图片通道，6是输出通道，3x3正方形卷积
        # 核（kernel）
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # 一个仿射操作：y = wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 128)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 在(2, 2)窗口上的最大池化
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 如果是正方形size可以指定一个数
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_feature(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return num_features

net = Net()
print(net)

输出：

Net(
(conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
(fc1): Linear(in_features=576, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)

你只需要定义一个forward函数，backward函数（计算梯度的函数）会自动使用autograd定义。你在forward函数里使用任何张量操作。

模型的可学习参数通过net.parameters()获得

1
2
3

params = list(net.parameters())
print(len(params))
print(params[0].size())     # conv1的权重

输出：

10
torch.Size([6, 1, 3, 3])

让我们尝试一个随机的32x32的输入。注意：这个网络（LeNet）期望输入的大小是32x32。在MNIST数据集上使用这个网络，请把数据集的图片的大小转换成32x32。

1
2
3

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

输出：

tensor([[ 0.0057, -0.0952,  0.1055, -0.0916, -0.1350,  0.0857, -0.0890,  0.0326,
        -0.0554,  0.1451]], grad_fn=<AddmmBackward>)

清零所有参数的梯度的缓冲和用随机的梯度进行反向传播。

1 2	net.zero_grad() out.backward(torch.randn(1, 10))

注意：
torch.nn只支持mini-batches(小的批处理)。整个torch.nn包只支持输入是样本的mini-batch，而不是单一的样本。
例如，nn.Conv2d将接受一个样本数x通道数x高x宽的四维张量。
如果你有一个单一的样本，只需使用input.unsqueeze(0)来增加一个伪batch维度。

在进行下一步之前，让我们重新回顾你目前看过的所有的类。

回顾：

torch.Tensor - 一个支持像是backward()的自动求导的多维数组。也保留关于这个张量的梯度。
nn.Module - 神经网络模块。封装参数的便捷方式。帮助他们移动到GPU，导出，加载等。
nn.Parameter - 一种Tensor，当它被分配给一个Module时，它会被自动注册为一个参数。
autograd.Function - 执行前向和一个自动求导操作的反向定义。每个Tensor操作创建至少一个单一的Function节点，与创建Tensor的和编码它的历史的函数。

至此，我们讨论了：

定义一个神经网络
执行了输入和调用反向传播

还剩下：

计算损失
更新网络的权重

损失函数

损失函数接受一对输入（output, target)，和计算输出与目标之间距离的值。

在nn包下有很多不同的损失函数。一个简单的损失是：nn.MSELoss,这个是计算输入和目标的均方误差。

例如：

output = net(input)
target = torch.randn(10)
target = target.view(1, -1)
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

输出：

tensor(0.9991, grad_fn=<MseLossBackward>)

现在，如果你使用它的.grad_fn属性沿着loss的方向向后移动，你将看到像这样的计算图：

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

所以，当我们调用loss.backward()，整个图对loss求导，并且图中所有有requires_grad=True的张量有一个累积梯度的.grad张量。

为了说明这一点，我们后退几步：

1
2
3

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0]) # Linear
print(loss.grad_fn.next_functions[0][0].next_function[0][0])   # Relu

输出：

<MseLossBackward object at 0x7ff716c28630>
<AddmmBackward object at 0x7ff716c28400>
<AccumulateGrad object at 0x7ff716c28400>

反向传播

为了反向传播误差我们必须做的全部只是调用loss.backward()。不过，您需要清除现有的梯度，否则梯度将累积为现有梯度。

现在，我们将调用loss.backward()，看一下conv1的偏置梯度在反向之前和之后的区别。

net.zero_grad()         # 清零所有参数的梯度缓冲

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

输出：

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0081,  0.0029,  0.0248, -0.0054,  0.0051,  0.0008])

现在，我们看如何使用损失函数。

我们剩下需要学习的是：

更新网络的权重

更新参数

在实践中使用的最简单的更新规则是随机梯度下降（SGD)。

1
2
3

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

然而，当你使用神经网络时，你想要使用不同的更新规则像是SGD，Nesterov-SGD，Adam，RMSProp等等。为了其中这些，你可以使用一个小的包：torch.optim来执行所有这些方法。使用它非常简单：

import torch.optim as optim

# 创建你的优化器
optimizer = optim.SGD(net.parameters(), lr = 0.01)

# 在训练循环里
optimizer.zero_grad()   # 清零梯度缓冲
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()        # 更新

注意：
观察到必须是手动地使用optimizer.zero_grad()清零梯度缓冲的。这是因为梯度是累积的，这个在反向传播里解释了。

训练一个分类器

[原英文网站]

就是这个。你已经看过如何定义神经网络，计算损失和更新网络的参数。

现在你可能会思考了，

那数据呢？

总体来说，当你不得不处理图片，文本，音频，视频数据，你可以使用标准的python库来把它们加载成numpy数组，然后你可以将数组转化成torch.*Tensor。

对于图像，像是Pillow,OpenCV包是有效的
对于音频，有scipy或librosa包
对于文本，原始的python或基于Cython加载，或NLTK和SpaCy都是有效的。

特别的对于视觉方面，我们已经创建了一个叫做torchvision的包，它提供了常见数据集（Imagenet，CIFAR10，MNIST等等）的数据加载器和图片的数据处理器，也就是torchvision.datasets和torch.utils.data.DataLoader。

这提供了很大的便利和避免了编写样本代码。

对于这个教程，我们将使用CIFAR10数据集。它有类别：飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船、卡车。CIFAR-10中的图片都是3x32x32的，也就是32x32像素大小、三颜色通道的图片。

cifar10

训练一个图片分类器

我们将依次进行下面的几步：

使用torchvision加载和标准化CIFAR10的训练集和测试集
定义卷积神经网络
定义损失函数
在训练集上训练神经网络
在测试集上测试网络

1.加载和规范化CIFAR10

使用torchvision，非常简单地加载CIFAR10

1
2
3

import torch
import torchvision
import torchvision.transforms as transforms

torchvision datasets输出是在范围[0, 1]的PILImage的图片。我们可以将他们处理成规范化过的范围在[-1, 1]的张量。

transform = transforms.Compose(
    [transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]
)

trainset = torchvision.datasets.CIFAR10(root='./data', train = True, download = True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4, shuffle=True, num_workers = 2)
testset = torchvision.datasets.CIFAR10(root='./data', train = True, download = True, transform = transform)
testloader = torch.utils.data.DataLoader(testset, batch_size = 4, shuffle=False, num_workers = 2)

classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

输出：

Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data/cifar-10-python.tar.gz
Extracting ./data/cifar-10-python.tar.gz to ./data
Files already downloaded and verified

让我们展示一些训练集图片。

import matplotlib.pyplot as plt
import numpy as np

# 展示图片的函数

def imshow(img):
    img = img / 2 + 0.5
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()


# 获得一些随机的训练集图片
dataiter = iter(trainloader)
images, labels = dataiter.next()

# 展示图片
imshow(torchvision.utils.make_grid(images))
# 打印标签
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

输出：

frog  ship   cat plane

2.定义一个卷积神经网络

从之前的神经网络章节复制神经网络，并且修改成三通道的图片（它之前定义的是一通道的图片）。

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5, 120)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return x

net = Net()

3.定义损失函数和优化器

让我们使用分类交叉熵损失和带有动量的SGD。

import torch.optim as optim

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr = 0.001, momentum = 0.9)

4.训练网络

这时事情变得有趣起来。我们简单地循环一下我们的数据迭代器，把输入喂给网络并且做优化。

for epoch in range(2):   # 循环几次数据集

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # 获得输入；数据是[输入，标签]的列表
        inputs, labels = data

        # 清零参数的梯度
        optimizer.zero_grad()

        # 前向+反向+优化
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # 打印统计信息
        running_loss += loss.item()
        if i % 2000 == 1999:    # 每2000个mini-batches打印一次
            print('[%d, %5d] loss: %.3f' % (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

输出：

[1,  2000] loss: 2.169
[1,  4000] loss: 1.808
[1,  6000] loss: 1.659
[1,  8000] loss: 1.553
[1, 10000] loss: 1.488
[1, 12000] loss: 1.455
[2,  2000] loss: 1.379
[2,  4000] loss: 1.346
[2,  6000] loss: 1.320
[2,  8000] loss: 1.305
[2, 10000] loss: 1.275
[2, 12000] loss: 1.262
Finished Training

5.在测试集上测试网络

我们已经在训练集上训练了两次网络。但是我们需要检测网络是否有学习。

我们将通过网络预测输出的类别标签检测这个，并且和事实做对比。如果预测是正确的，我们向正确预测的列表里添加该样本。

OK，第一步。让我们从测试集中取出图片来展示熟悉一下。

dataiter = iter(testloader)
images, labels = dataiter.next()

# 打印图片
imshow(torch.vision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

输出：

GroundTruth:    cat  ship  ship plane

ok，现在让我们看看神经网络认为上面的例子是什么：

1	output = net(images)

输出是这10类的信念值（energies）。越高信念值的一类，模型越认为图片是这一类。所以，让我们最高信念值的标签：

1 2	_, predicted = torch.max(output, 1) print('Predicted:', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))

输出：

Predicted:    cat plane plane  ship

结果看起来不错。

让我们看一下网络在整个数据集上表现怎么样。

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

输出：

Accuracy of the network on the 10000 test images: 54 %

看起来比碰运气（10%的准确率，从10类中随机选一类）要好的多。像是网络已经学习了一些东西。

嗯~，哪些类表现的好，哪些类表现的不好呢：

class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(4):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1


for i in range(10):
    print('Accuracy of %5s : %2d %%' % (
        classes[i], 100 * class_correct[i] / class_total[i]))

输出：

Accuracy of plane : 46 %
Accuracy of   car : 63 %
Accuracy of  bird : 50 %
Accuracy of   cat : 37 %
Accuracy of  deer : 40 %
Accuracy of   dog : 51 %
Accuracy of  frog : 70 %
Accuracy of horse : 48 %
Accuracy of  ship : 76 %
Accuracy of truck : 64 %

ok，那下一步干什么？

我们如何在GPU上运行神经网络？

在GPU上训练

就像如何把张量移动到GPU上，把神经网络移动到GPU上。

如果我们有可用的CUDA，首先让我们定义设备为第一个可得到的cuda设备。

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# 假设我们有一个CUDA机器，然后我们打印CUDA设备：

print(device)

输出：

cuda:0

这个章节的剩余内容都假设device是一个CUDA设备。

然后这些方法将在所有module上递归运行，把它们的参数和缓冲转换成CUDA tensors。

1	net.to(device)

记得你也要将每次迭代的输入和标签都送到GPU：

1	inputs, labels = data[0].to(device), data[1].to(device)

为什么我没有注意到与CPU相比的巨大加速?因为你的网络真的很小。

练习: 尝试增加网络的宽度（第一个nn.Conv2d的参数2和第二个nn.Conv2d的参数1必须相等），看看你得到怎样的加速。

已完成的目标:

高层次地理解了pytorch张量的库和神经网络
训练了一个小的图片分类的神经网络

在多GPU上训练

如果你想使用你全部的GPU看到巨大的加速，请参考下一章节

选读：数据并行

[原英文网站]

在这个教程里，我们将使用DataParallel学习如何使用多个GPUS（译者注：一机多卡）

pytorch很容易实现多GPU。你能把模型放到一个GPU上：

1 2	device = torch.device("cuda:0") model.to(device)

然后你可以把你的所有数据放到GPU上：

1	mytensor = my_tensor.to(device)

请注意只是调用my_tensor.to(device)返回一个新的在GPU上的my_tensor的拷贝，而不是覆盖my_tensor。你需要分配一个新的tensor并使用这个在GPU上的tensor。

在多GPU上执行正向和反向传播是很自然的。然而，pytorch将默认使用一个GPU。你可以使用DataParallel使你的模型并行运行来简单地在多GPU上运行你的操作。

1	model = nn.DataParallel(model)

这就是本教程的核心。我们将在下面更详细地探讨它。

引入和参数

引入pytorch模块和定义参数。

import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader

# Parameters and DataLoaders
input_size = 5
output_size = 2

batch_size = 30
data_size = 100

设备：

1	device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

虚拟数据集

建立一个虚拟（随机）的数据集，你只需执行getitem。

class RandomDataset(Dataset):

    def __init__(self, size, length):
        self.len = length
        self.data = torch.randn(length, size)

    def __getitem__(self, index):
        return self.data[index]

    def __len__(self):
        return self.len

rand_loader = DataLoader(dataset=RandomDataset(input_size, data_size),
                         batch_size=batch_size, shuffle=True)

简单的模型

作为小样，我们的模型只需获得输入，执行线性操作，然后得出输出。然而，你能使用DataParallel在任何模型上(CNN, RNN, Capsule Net等等。)

我们在模型中放置了一个print语句来监视输入和输出张量的大小。请注意批号为0的打印内容。

class Model(nn.Module):
    # Our model

    def __init__(self, input_size, output_size):
        super(Model, self).__init__()
        self.fc = nn.Linear(input_size, output_size)

    def forward(self, input):
        output = self.fc(input)
        print("\tIn Model: input size", input.size(),
              "output size", output.size())

        return output

创建模型和数据并行

这是本教程的核心内容。首先，我们需要创建一个模型实例和检查是否有多个GPU。如果我们有多个GPU，我们可以使用nn.DataParallel封装你的模型。然后我们把模型通过model.to(device)放到GPU上。

model = Model(input_size, output_size)
if torch.cuda.device_count() > 1:
  print("Let's use", torch.cuda.device_count(), "GPUs!")
  # dim = 0 [30, xxx] -> [10, ...], [10, ...], [10, ...] on 3 GPUs
  model = nn.DataParallel(model)

model.to(device)

输出：

Let's use 2 GPUs!

运行模型

现在我们看一下输入和输出张量的大小。

for data in rand_loader:
    input = data.to(device)
    output = model(input)
    print("Outside: input size", input.size(),
          "output_size", output.size())

输出：

In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
        In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
        In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
        In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
        In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
        In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
        In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
        In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])

结果

如果你没有或一个GPU，当你批处理30个输入，模型会得到30个预期的输出。但是如果你有多GPU，然后你会得到像这样的结果。

2 GPUs

如果你有2个，你将看到：

Let's use 2 GPUs!
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
    In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
    In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])

3GPUs

如果你有3个GPU，你将看到：

Let's use 3 GPUs!
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
    In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])

8GPUs

如果你有8个，你将看到：

Let's use 8 GPUs!
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
    In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])

总结

DataParallel会自动地分割你的数据，并将工作订单发送到多个gpu上的多个模型。在每个模型完成它们的工作后，DataParallel收集并合并结果，然后返回给你。

———————————————感谢阅读———————————————